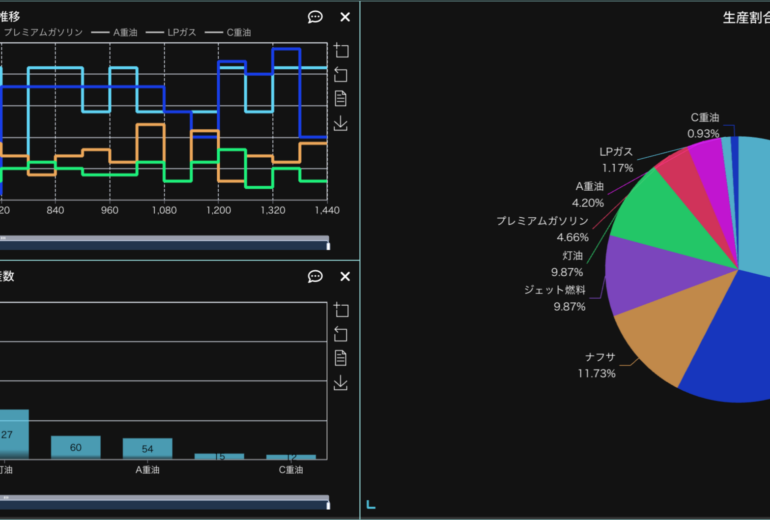
概要
今回の記事では、assimeeの入荷データの生成に関数を使用する方法を、正規分布(ガウス分布)を例にして説明します。通常、時系列データに正規分布を想定することはありません。これは正規分布には負の領域が含まれる可能性が常にあるためで、本来は正の領域のみを持つガンマ分布等を使用する必要あります。
今回の記事では解説を簡潔にするため、需要(入荷)を関数として想定する場合の例に最も基本的な正規分布(ガウス分布)を使用していることに留意してください。
正規分布とは
正規分布とは確率分布関数の中で最も簡単で一般的に使われる関数の事を言います。この正規分布は自然界や社会科学など多くの現象をモデル化する際に利用されます。
正規分布の特徴と関数
正規分布を簡単に解説します。正規分布(ガウス分布)の確率分布関数f(x)は以下の式で表されます。
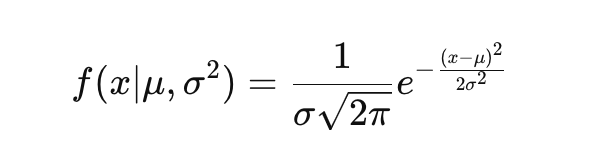
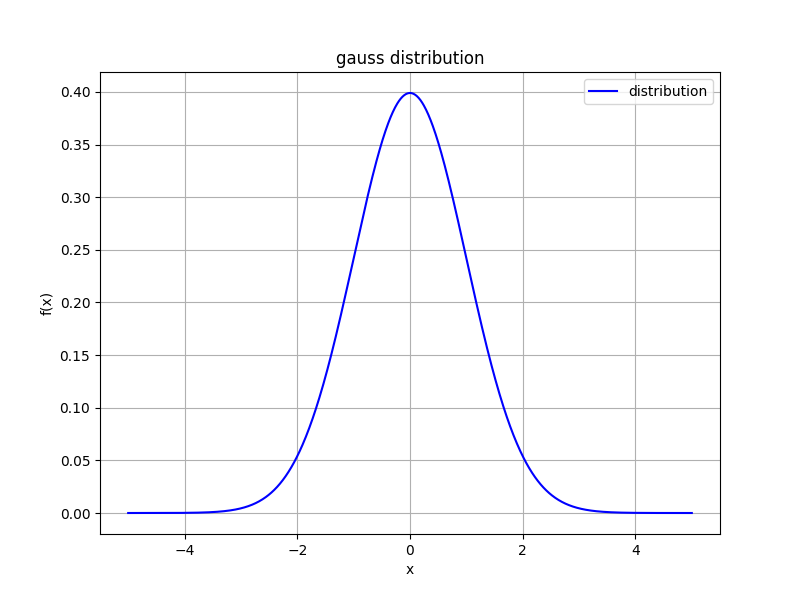
この関数は以下の特徴を持ちます。
- 平均値(μ)とxの最頻値、xの中央値が一致する
- 平均値を中心に左右対称(xが0の場合、正負両方向に同等な分布が出来る)
- 左右に広がる確率分布は0へ漸減する
- 標準偏差(σ)が大きくなると山が低く平べったくなり大きく外れたデータが増える
正規分布に対応した入荷データの作成
今回使用する疑似的な入荷データをエクセルを利用して生成します。
まず、エクセルで適宜ファイルを作成し、以下のようにSheet1に正規分布の確率分布関数を制御する平均値(μ)と標準偏差(σ)を用意します。今回の記事では入荷時間に当たるxの平均値を150、標準偏差を50としました(これらは任意に変更することが可能です)。

次にデータサンプルを生成します。エクセルファイルのSheet2へ移り、Sheet1で定義した変数(平均値、標準偏差)とエクセル組み込みの正規分布関数の逆関数NORMINV(確率、平均、標準偏差)に確率に相当する乱数を発生させる関数RAND()を使ってデータを生成する以下の数式をA1セルへ入力します。

その後、数式を任意の数のセルにコピーしてきます。ここでは500セル分をコピーしました。これによりSheet1の確率分布関数に従うランダムなデータを500個生成することが出来ました。
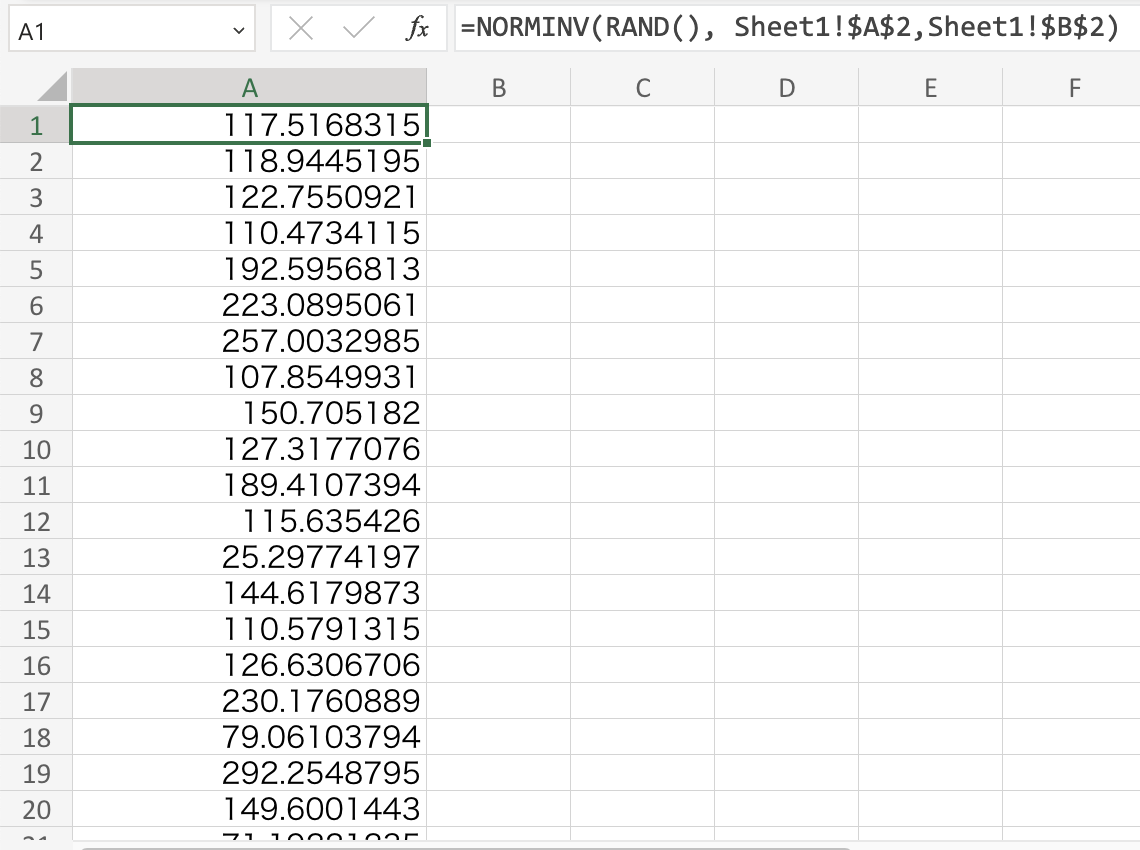
入荷データの度数の計算
Sheet1に戻り、時間に対する度数(入荷数)の分布を計算します。これは生成した入荷データがどの区間に属しているかを分別して、時間毎に発生したデータの数を数える作業になります。これもエクセルを使って以下のようにデータ区間を用意し、各データ区間の時間の上限値、下限値、中央値=(上限値+下限値)/2を用意します。今回のデータ区間は60分区切りとしました。
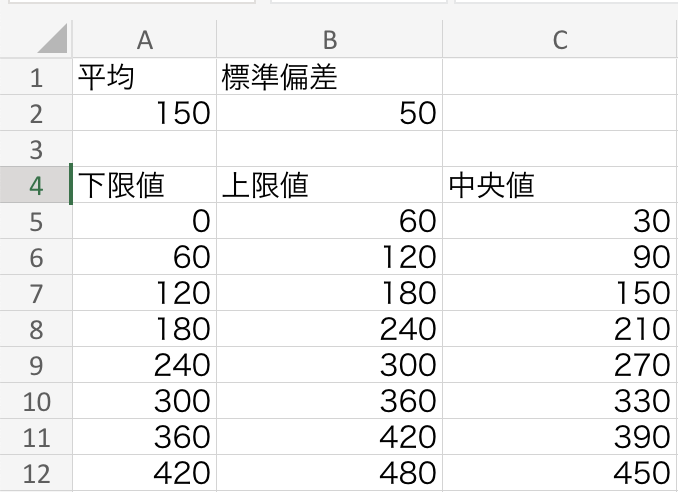
次にデータ区間の中央値の隣のセルにそれぞれの区間に入るデータの数(度数)の計算式を以下のように入力します。これはSheet2のデータのうち、各データ区間の上限値と下限値の間にあるデータの数を数え上げる計算式で、(データ区間の下限値以上のデータ数)ー(データ区間の上限値以上のデータ数)を計算しています。
*この式はデータがSheet2のA1からA500まであることを仮定しているので、データが500ではないなどの変更があった場合は適宜修正して下さい。
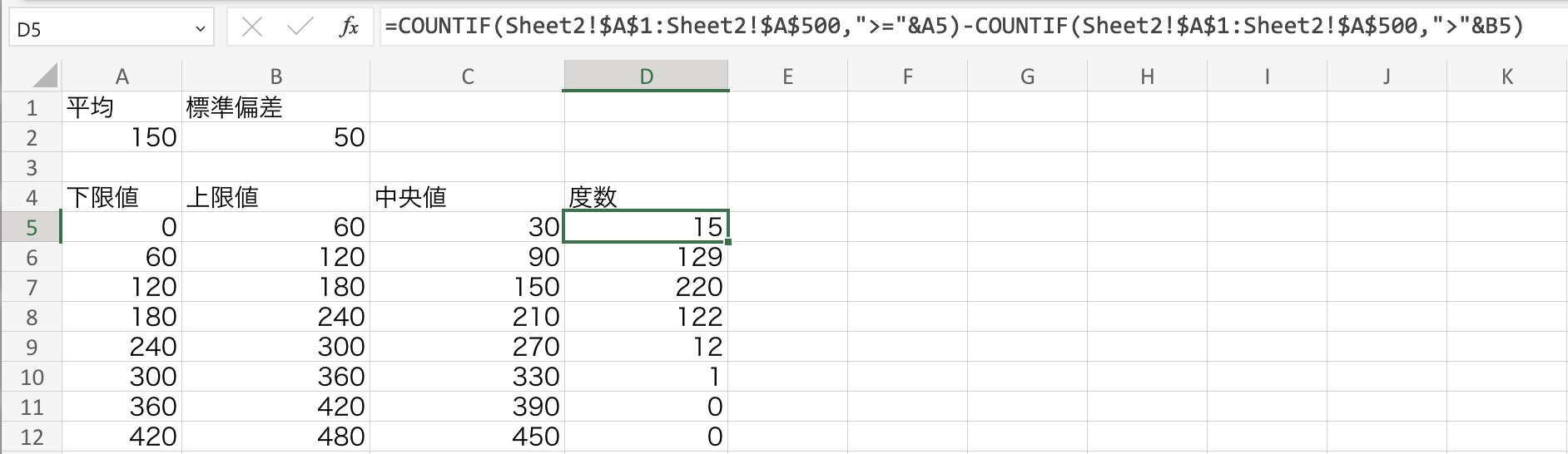
この計算式は先ほど定義したデータ区間の上限値(上の図ではB5)、下限値(上の図ではA5)、Sheet2のデータを引用するように作ってあるので、このセルをカットアンドペーストすることで、度数分布を簡単に生成することが出来ます。
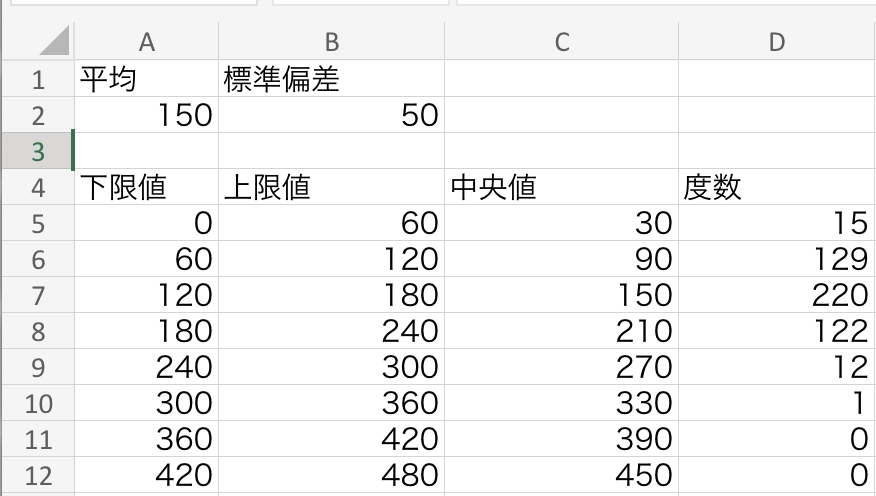
次に度数分布の確認のため、エクセルのグラフ機能を利用し、縦軸に度数、横軸にデータ区間の中央値を取って度数(入荷数) のグラフを作成します。
*今回、利用した度数の総数は499個でした。残りの1個は分布の平均値から大きく外れたデータ区間外にあると考えられます。これを回避したい場合は正規分布の正の部分だけを使用するガンマ分布等を利用する、データの平均値の設定(今回は150)を十分に大きくする(以上、外れデータが負の場合)、マイナスも含めデータ区間を広く設定する(データが両側に外れる場合)などが考えられます。
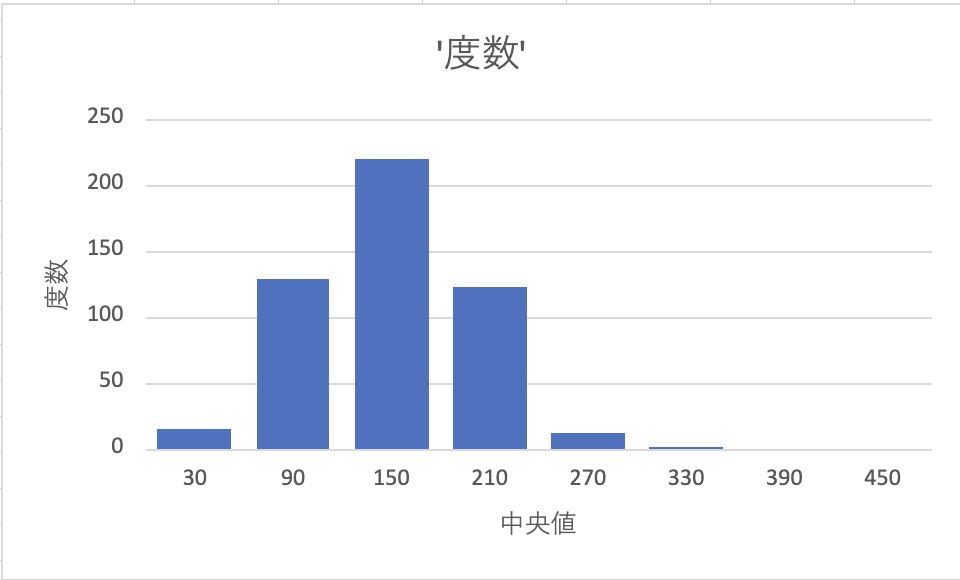
グラフが上のように表示されれば、150分を中心として度数分布が生成されていることが分かります。今回用意したエクセルシートは入荷時間や標準偏差を変えることで、様々な入荷時間に対応した入荷分布を作成することが出来ます。
*正規分布では中央値が0に近付くほど、xが負となる領域が大きくなります(x=0では半分が負)。これはxが時間で、x=0を中央値として分布を生成するような場合に特に問題になります。このような場合には冒頭にあるようにxの正の部分のみを使ったガンマ分布等を利用するべきですが、今回は解説を簡潔にするために最も単純な正規分布(ガウス分布)を使用していることに注意してください。
モデル作成
モデル
今回シミュレーションを行う分布は以下のようなモデルです。

想定条件
- 入荷は発注書として取り扱う
- 発注書に応じて商品を発送する
STEP1:プロセス図の作成
入荷プロセス:
特に変更なし
置き場プロセス:
プロセス名を「発注書置き場」へ変更
加工プロセス:
プロセス名を「商品準備」へ変更
置き場プロセス:
プロセス名を「商品置き場」へ変更
運搬(人)プロセス:
特に変更なし
出荷プロセス:
特に変更なし
STEP2:パラメーターの設定
001入荷:
品目名を「発注書」として入荷データを以下のように設定
入荷データの設定
入荷の詳細設定から以下のように生成した度数分布に従ってデータを入力します。*生成したエクセルのデータを境目が分かりやすいように60分ずらして入力しています。
| 時間 | 入荷数 |
| 0 | 0 |
| 60 | 15 |
| 120 | 129 |
| 180 | 220 |
| 240 | 122 |
| 300 | 12 |
| 360 | 1 |
| 420 | 0 |
| 480 | 0 |
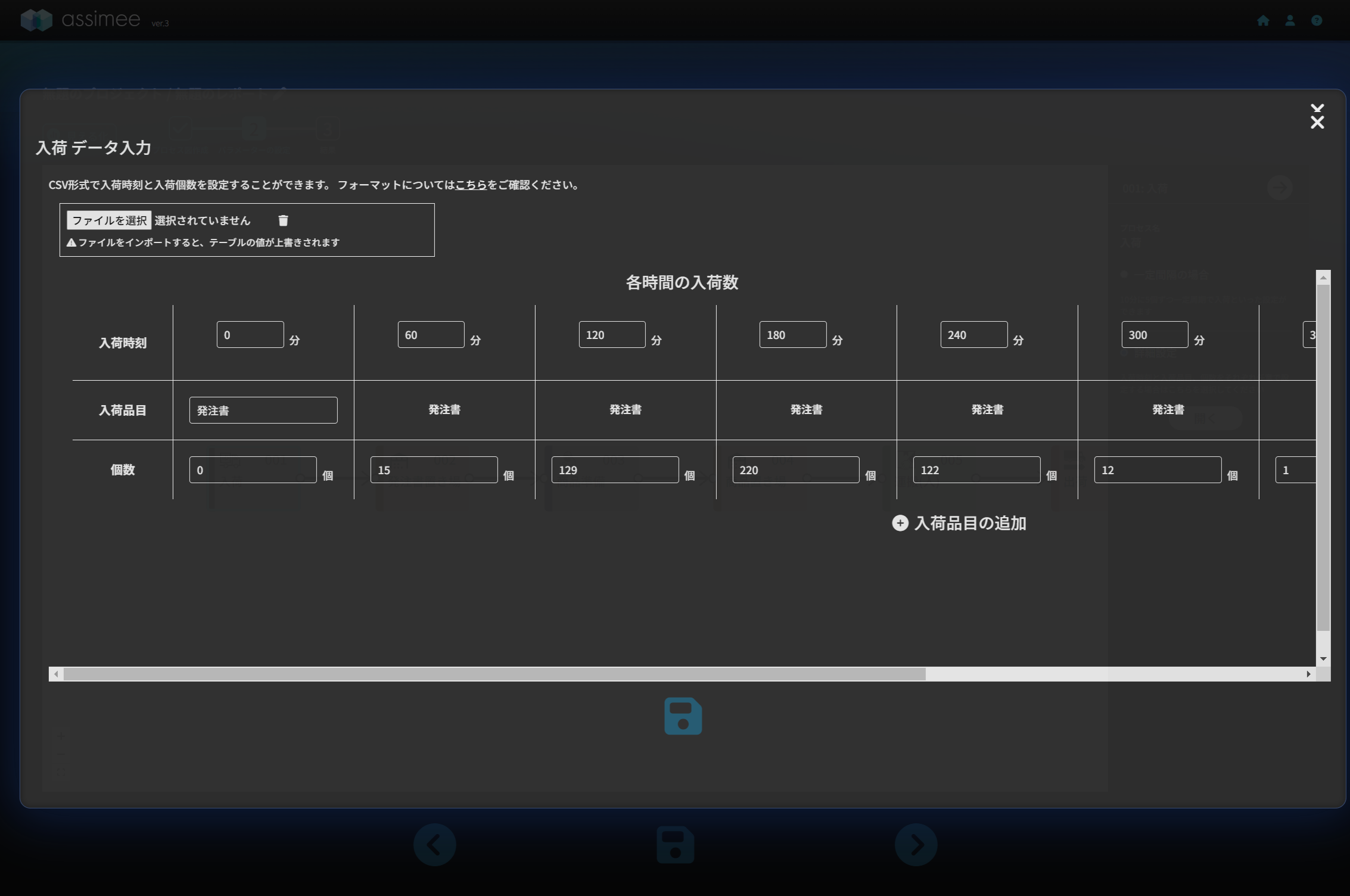
002発注書置き場:
容量を「1000個」と設定
003商品準備:
1回あたりの処理時間を「10分」、詳細設定を開き、作業員にチェックを入れ人数を「20人」と設定
対象品目名称を「発注書」、個数を「1個」、
出力品目名称を「商品」、個数を「1個」と設定
004商品置き場:
容量を「1000個」と設定
005運搬(人):
最大運搬量を「20個」、搬送時間(片道)を「5分」、人数を「10人」と設定
006出荷:
特に変更なし
シミュレーション
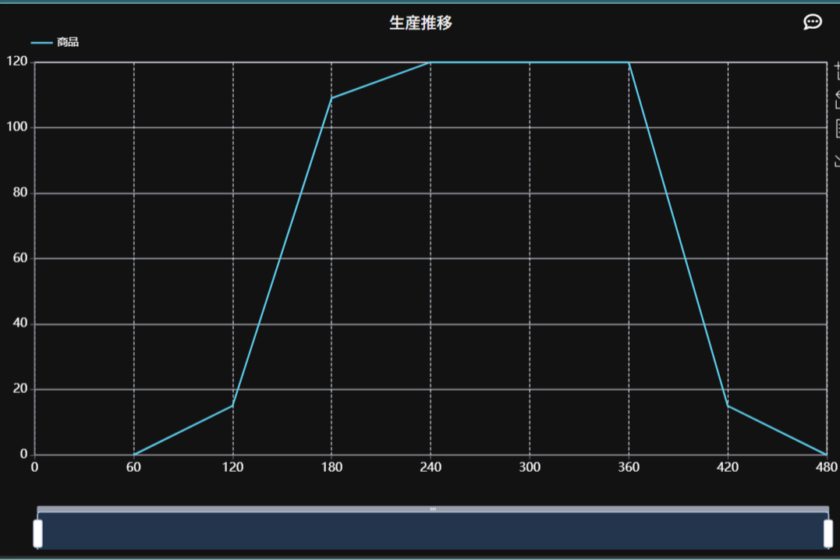
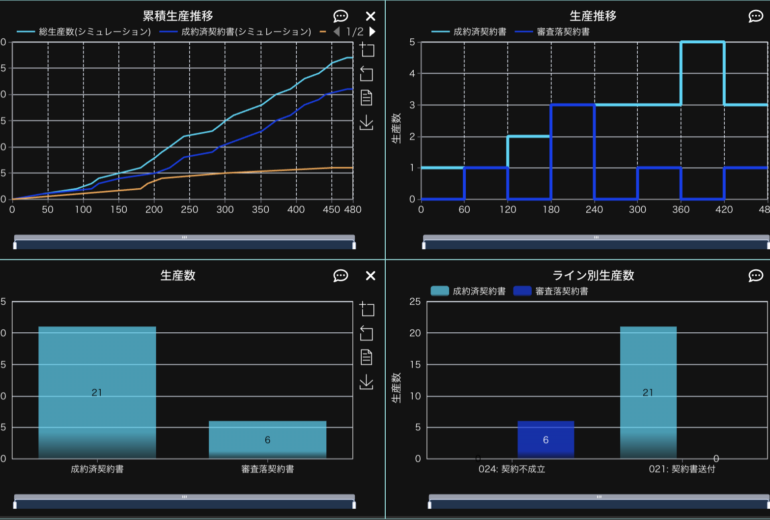
モデルを作成したらシミュレーションを行います。今回は480分の設定でシミュレーションを行います。パラメーターが問題なく設定されていれば、以下のような入荷結果とシミュレーション結果が表示されます。
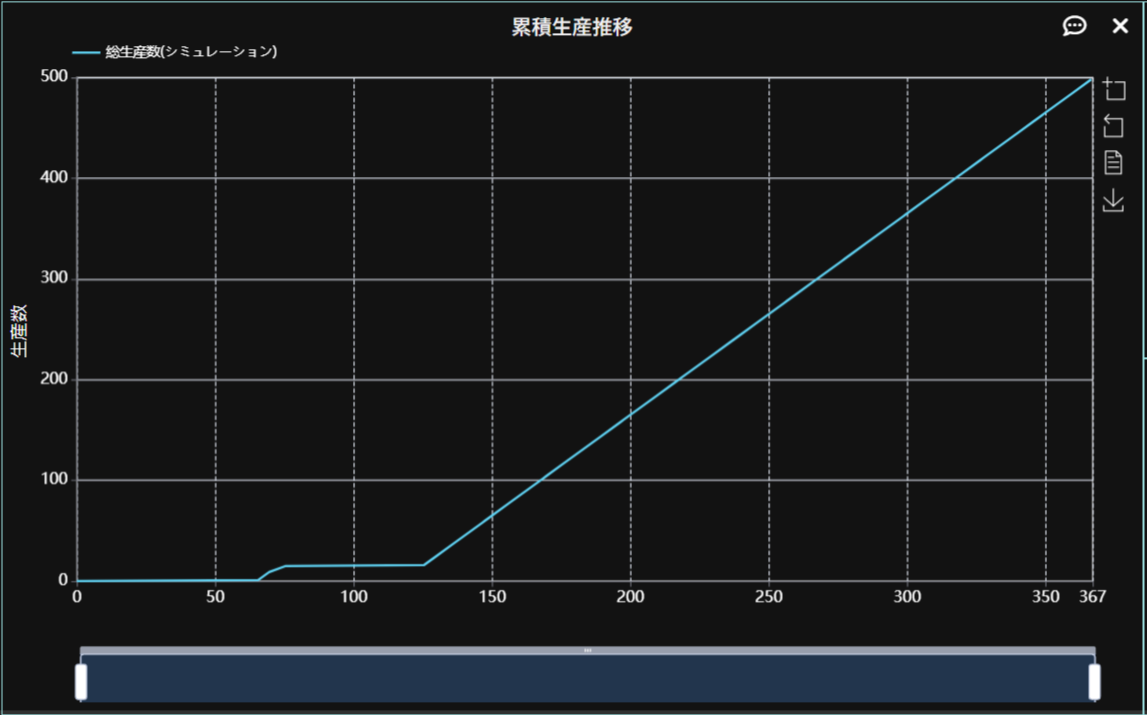
「001入荷」をクリックすることで確認できる入荷結果からは60分ごとに想定通り入荷が行われていることが確認できます。
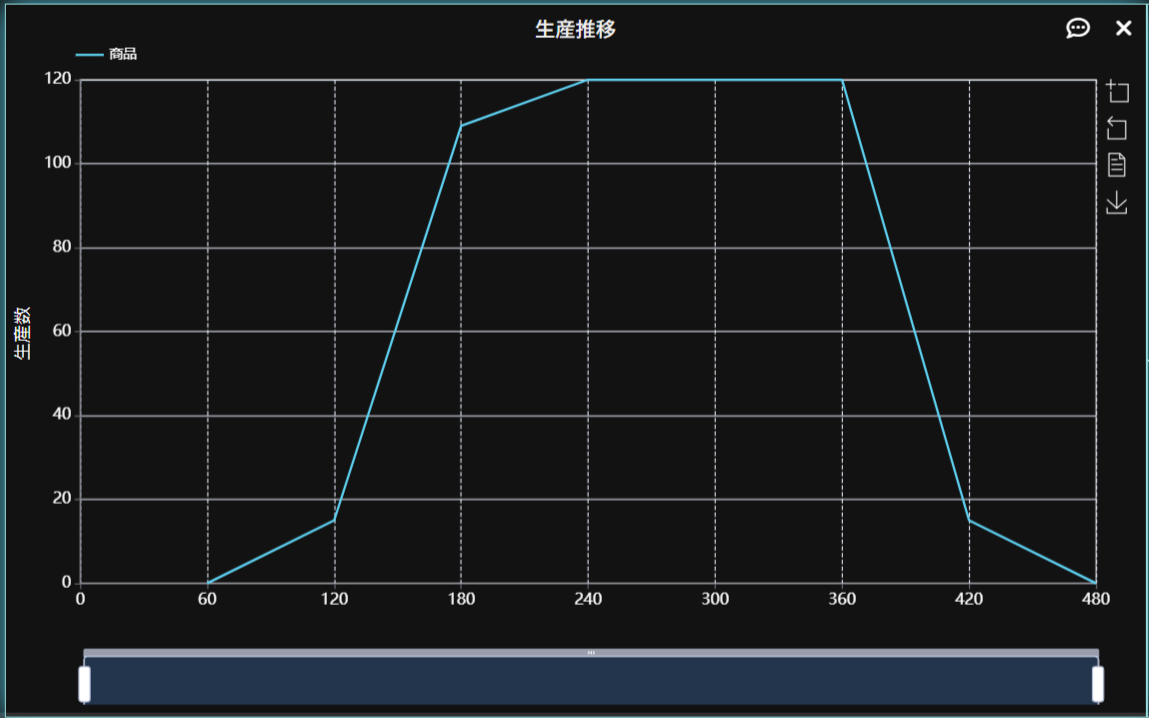
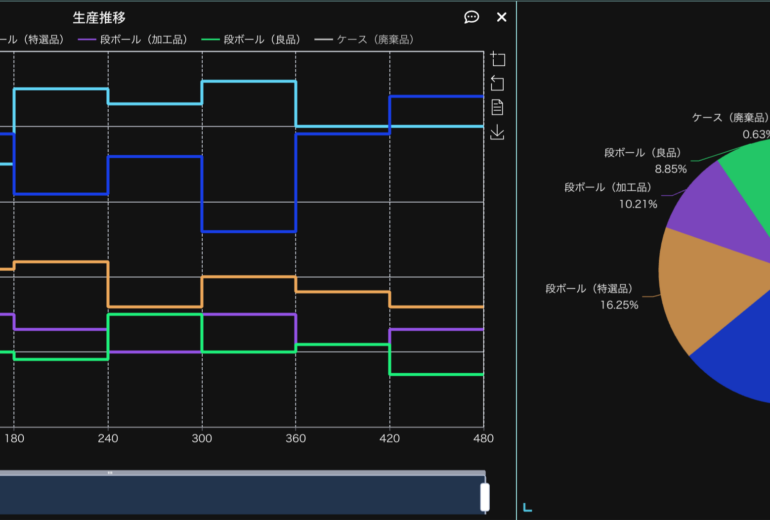
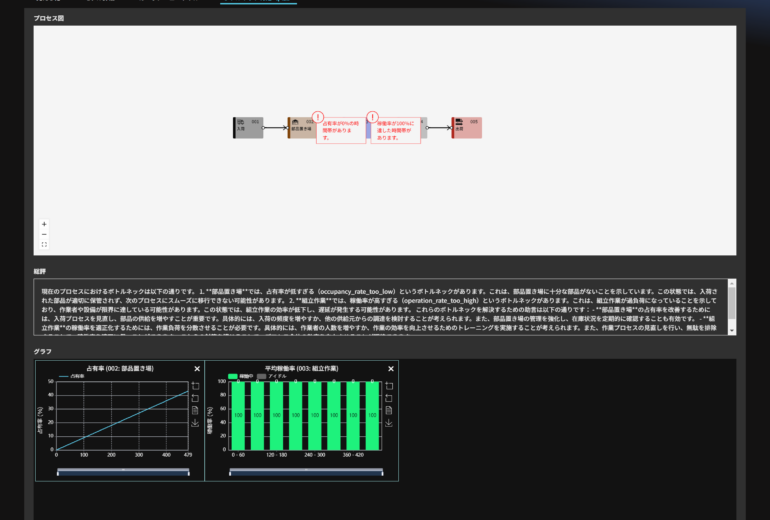
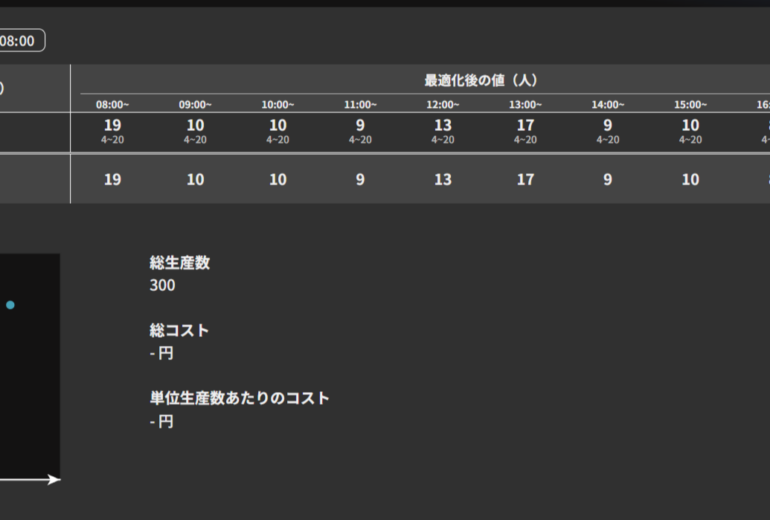
シミュレーション結果は上図のようになります。総生産数のピークは210分(入荷データでずらした60分+正規分布の平均値の150分)に出るはずですが、入荷後の加工処理の時間や運搬時間があるため、後へスライドしていることがわかります。また、120個の出荷が上限になっていますが、これはプロセス処理上の上限値であることが他のプロセス、003加工のパラメーターや稼働率の確認から分かります(003加工では20分かかる処理を10人で行うため、1分間あたり2個の加工が上限)。
まとめ
今回はエクセルで正規分布関数に従ったデータを生成し、入荷数(需要)として扱う方法について解説しました。このように解析的にデータを計算して用意することで、正規分布以外の様々な関数を利用することが可能となり、多彩な入力をassimeeで利用することが出来ます。
assimeeでは、実際の製造プロセスをモデル化し、シミュレーションすることで、プロセスの見える化や潜在的な課題の洗い出しを行うことができます。製造プロセスのデジタル化や課題解決でお悩みの方は、ぜひお問い合わせください。